Answer:
The standard deviation of the number of education majors in the sample is of 3.34.
Step-by-step explanation:
The students are chosen without replacement, which means that the hypergeometric distribution is used to solve this question.
Hypergeometric distribution:
The probability of x successes is given by the following formula:
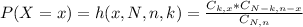
In which:
x is the number of successes.
N is the size of the population.
n is the size of the sample.
k is the total number of desired outcomes.
Combinations formula:
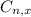 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
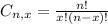
Standard deviation:
The standard deviation of the hypergeometric distribution is:
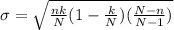
In this question:
300 freshmen means that
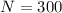
110 are education majors, which means that
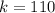
60 are chosen, which means that

Find the standard deviation of the number of education majors in the sample.
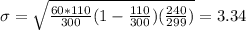
The standard deviation of the number of education majors in the sample is of 3.34.