Question

Assume that thermometer readings are normally distributed with a mean of 0 degrees C and a standard deviation of 1.00 degrees C. A thermometer is randomly selected and tested. For the case below, draw a sketch, and find the probability of the reading. (The given values are in celsius degrees)

Between -1.42 and 1.61
The probability of getting a reading between -1.42 degrees C and 1.61 degreesC is_______ ( round to four decimal places as needed)

Answer 1

The probability of getting a reading between -1.42 degree C and 1.61 degree C is 0.8685.

Explanation:

We are given that

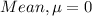`Mean,\mu=0` degree C

Standard deviation,
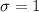`\sigma=1` degree C

We have to find the probability of the reading between -1.42 and 1.61.

`P(-1.42<x<1.61)=P((-1.42-0)/(1)<(x-\mu)/(\sigma)<(1.61-0)/(1))`

`P(-1.42<x<1.61)=P(-1.42<Z<1.61)`

`P(-1.42<x<1.61)=P(Z<1.61)-P(Z<-1.42)`

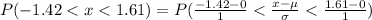
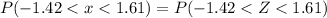
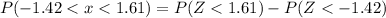
Using the formula

`P(a<z<b)=P(z<b)-P(z<a)`

`P(-1.42<x<1.61)=0.94630-0.07780`

`P(-1.42<x<1.61)=0.8685`

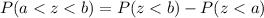
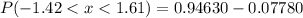
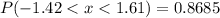
Hence, the probability of getting a reading between -1.42 degree C and 1.61 degree C is 0.8685.