Question

A ladder is placed 8 feet away from a wall. The distance from the ground straight to the top of the wall is 16 feet. What is the height of the ladder?

Answer 1

`\boxed{\large{\bold{\blue{ANSWER~:) }}}}`

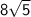
Given:-

• A ladder is placed 8 feet away from a wall. The distance from the ground straight to the top of the wall is 16 feet.

Find:-

• What is the height of the ladder?

solution:-

A ladder is placed 8 feet away from a wall. The distance from the ground straight to the top of the wall is 16 feet.

so it is a right angle triangle

we know that,

in a right angle triangle, According to the Pythagorean theorom,

`\boxed{\sf{l^2+b^2=h^2 }}`

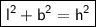
where

• l= legs
• b=base
• h=hypotenuse

According to the question,

• 
  `\sf{8^2+16^2=h^2 }`

• 
  `\sf{64+256=h^2 }`

• 
  `\sf{ h^2=320 }`

• 
  `\sf{h=√(320) }`

• 
  `\sf{h=8√(5) }`

Therefore:-

The height of the ladder is
`\sf{8√(5) }`

Answer 2

17.89 ft

Explanation:

This is a right triangle so we can use the Pythagorean theorem

a^2 + b^2 = c^2 where a and b are the legs and c is the hypotenuse

8^2 +16^2 = c^2

64+ 256 = c^2

320 =c^2

Taking the square root of each side

sqrt(320) = sqrt(c^2)

sqrt(64*5) = c

sqrt(64) sqrt(5) =c

8 sqrt(5) = c

17.88854382=c

17.89 ft