Answer:
1. c. Poisson
2. 0.9592 = 95.92% probability that in any one minute at least one purchase is made.
3. 0.0017 = 0.17% probability that no one makes a purchase in the next 2 minutes.
Explanation:
We have only the mean, which means that the Poisson distribution is used to solve this question, and thus the answer to question 1 is given by option c.
Poisson distribution:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given interval.
is the mean in the given interval.
Mean of 3.2 minutes:
This means that
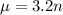 , in which n is the number of minutes.
, in which n is the number of minutes.
2. What is the probability that in any one minute at least one purchase is made?
 , so
, so
 .
.
This probability is:
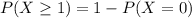
In which

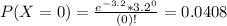
So

0.9592 = 95.92% probability that in any one minute at least one purchase is made.
3. What is the probability that no one makes a purchase in the next 2 minutes?
2 minutes, so
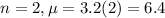
This probability is P(X = 0). So

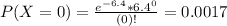
0.0017 = 0.17% probability that no one makes a purchase in the next 2 minutes.