Answer:
Part A)
50
Part B)
1
Part C)
50 feet per second.
Explanation:
First, note that Point A is at (3, 150) and that Point B is at (4, 200).
Part A)
The y-values of Point A and Point B are 150 and 200, respectively.
Therefore, the change in y-value from A to B is:
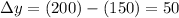
(Note, the triangle symbol or Greek letter Delta is used to denote "change" or "difference.")
Part B)
The x-values of Point A and Point B are 3 and 4, respectively.
Therefore, the change in x-value from A to B is:
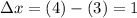
Part C)
Recall that the rate of change of a linear function is given by the change of y over the change of x. In other words:
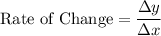
Substitute and evaluate:
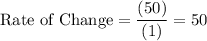
Since the y-values are in feet and the x-values are in seconds, the rate of change of the linear function is 50 feet per second.