Answer:
The distance between two points (a, b) and (c, d) is given by:

So the distance between the point (6, 5) and the line y = 5x - 10 can be thought as the distance between the point (6, 5) and the point (x, 5x - 10)
Where:
(x, 5x - 10) denotes all the points in the line y = 5x – 10
That distance is given by:
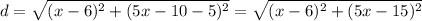
Now we want to minimize this.
Because the distance is a positive quantity, we can try to minimize d^2 insted, so we have:
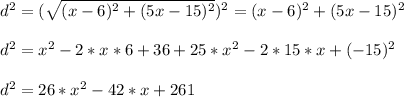
Notice that this is a quadratic equation with a positive leading coefficient, which means that the arms of the graph will open upwards, then the minimum will be at the vertex of the parabola.
Remember that for a parabola:
y = a*x^2 + bx + c
the x-value of the vertex is:
x = -b/2a
Then for our parabola:
d^2 = 26*x^2 - 42*x + 261
The vertex is at:
x = -(-42)/(2*26) = 0.808
Then we just need to evaluate the distance equation in that value of x to get the shortest distance:
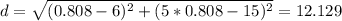
The shortest distance between the point A and the line is 12.129 units.