Answer:
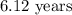
Explanation:
Given
Rate of interest is
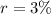 compounded quarterly
compounded quarterly
So, annually it is
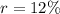
Suppose
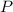 is the Principal and A is the amount after certain time period.
is the Principal and A is the amount after certain time period.
Amount in Compound interest is given by
![\Rightarrow A=P[1+r\%]^t](https://img.qammunity.org/2022/formulas/mathematics/high-school/f5l8fa77sd403frkmi97zuvh713xgnz24j.png)
for given conditions
![\Rightarrow 2P=P[1+0.12]^t\\\Rightarrow 2=(1.12)^t\\\\\Rightarrow t=(\ln (2))/(\ln (1.12))\\\\\Rightarrow t=6.116\approx 6.12\ \text{years}](https://img.qammunity.org/2022/formulas/mathematics/college/zwktp4alh13krm7xleutfmrlq1wp0ebs4d.png)
It take
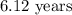 to double the invested amount.
to double the invested amount.