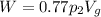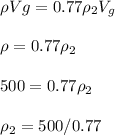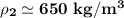Question

A uniform plastic block floats in water with 50.0 % of its volume above the surface of the water. The block is placed in a second liquid and floats with 23.0 % of its volume above the surface of the liquid.

What is the density of the second liquid?
Express your answer with the appropriate units.

Answer 1

density of second liquid = 650 kg/m³

Step-by-step explanation:

Given that:

The volume of the plastic block submerged inside the water = 0.5 V

The force on the plastic block =
`\rho_1V_1g`

`= 0.5p_1 V_g`

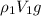
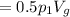
when the block is floating, the weight supporting the force (buoyancy force) is:

W
`= 0.5p_1 V_g`

`\rho Vg = 0.5p_1 V_g`

`\rho = 0.5 \rho _1`

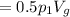
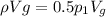
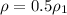
where;

water density
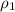`\rho _1` = 1000

`\rho = 0.5 (1000)`

`\rho = 500 kg/m^3`

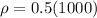
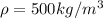
In the second liquid, the volume of plastic block in the water = (100-23)%

= 77% = 0.7 V

The force on the plastic block is:

`= 0.77p_2 V_g`

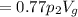
when the block is floating, the weight supporting the force (buoyancy force) is:

`W = 0.77p_2 V_g`

`\rho Vg = 0.77 \rho_2 V_g \\ \\ \rho = 0.77 \rho_2 \\ \\ 500 = 0.77 \rho_2 \\ \\ \rho_2 = 500/0.77`

`\mathbf{ \rho_2 \simeq 650 \ kg/m^3}`