Question

A fruit company delivers its fruit in 2 types of boxes: large and small. A delivery of 3 large boxes and 5 small boxes has a total weight of 79 kilograms. A delivery of 12 large boxes and 2 small boxes has a total weight of 199 kilograms. How much does each type of box weight?

Answer 1

9514 1404 393

Answer:

• large: 15.5 kg
• small 6.5 kg

Explanation:

Let x and y represent the weights of the large and small boxes, respectively. Then the two delivery weights give rise to the equations ...

3x +5y -79 = 0

12x +2y -199 = 0

Using the "cross multiplication method" of solving these equations, we find ...

d1 = (3)(2) -(12)(5) = 6 -60 = -54

d2 = 5(-199) -(2)(-79) = -995 +158 = -837

d3 = -79(12) -(-199)(3) = -948 +597 = -351

1/d1 = x/d2 = y/d3

x = d2/d1 = -837/-54 = 15.5

y = d3/d1 = -351/-54 = 6.5

The large boxes weigh 15.5 kg; the small boxes weigh 6.5 kg.

_____

Additional comment

My preferred quick and easy way to solve equations like this is using a graphing calculator. In addition to that, an algebraic method is shown.

The "cross-multiplication method" shown here is what I consider to be a simplified version of what you would find in videos. It is a variation of Cramer's rule and the Vedic maths methods of solving pairs of linear equations. I find it useful when "elimination" or "substitution" methods would result in annoying numbers. In such cases, it uses fewer arithmetic operations than would be required by other methods.

Short description: writing the coefficients of the general form equations in 4 columns, where the last column is the same as the first, a "cross multiplication" is computed for each of the three pairs of columns. Those computations are of the form ...

`\text{column pair: }\begin{array}{cc}a&b\\c&d\end{array}\ \Rightarrow\ d_n=ad-cb`

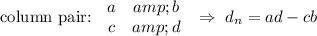
The relationship between the differences d₁, d₂, and d₃ and the variable values is shown above.