Answer:
A) 10%
Explanation:
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Sam's monthly bills are normally distributed with mean 2700 and standard deviation 230.9.
This means that
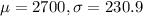
What is the probability that his expenses will exceed his income in the following month?
Expenses above 2*1500 = $3000, which is 1 subtracted by the p-value of Z when X = 3000.

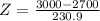
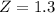
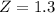 has a p-value of 0.9032.
has a p-value of 0.9032.
1 - 0.9032 = 0.0968 that is, close to 10%, and thus the correct answer is given by option A.