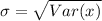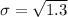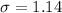Answer:
(1)

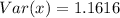
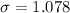
(2)
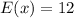
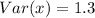
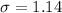
Explanation:
Solving (1):
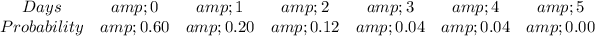
(a): Mean
This is calculated as:

So, we have:
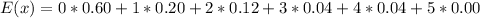

Solving (b): The variance
This is calculated as:
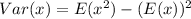
Where:

and
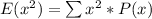
So, we have:
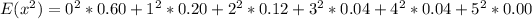
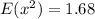
So, we have:
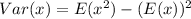
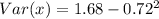
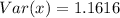
Solving (c): The standard deviation.
This is calculated as:
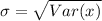
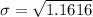
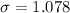
Solving (2):

(a): Mean
This is calculated as:

So, we have:
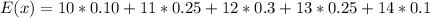
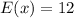
Solving (b): The variance
This is calculated as:
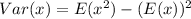
Where:
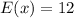
and
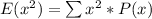
So, we have:

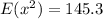
So, we have:
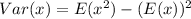
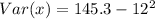
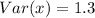
Solving (c): The standard deviation.
This is calculated as: