Question

Seventeen individuals are scheduled to take a driving test at a particular DMV office on a certain day, nine of whom will be taking the test for the first time. Suppose that six of these individuals are randomly assigned to a particular examiner, and let X be the number among the six who are taking the test for the first time. (a) What kind of a distribution does X have (name and values of al parameters)? 17 hx;6, 9, 17) O h(x; 6,? 17 bx; 6, 9,17) (x; 6, 9, 17) 17 (b) Compute P(X = 4), P(X S 4), and P(X PLX = 4) 0.2851 PX S 4)-13946X RX24) -0.1096 X 4). (Round your answers to four decimal places.) (c) Calculaethe mean value and standard deviation of X. (Round your answers to three decimal places.)

Answer 1

a) h(x; 6, 9, 17).

b) P[X=2] = 0.2036

P[X ≤ 2] = 0.2466

P[X ≥ 2] = 0.9570.

c) Mean = 3.176.

Variance = 1.028.

Standard deviation = 1.014.

Explanation:

From the given details K=6, n=9, N=-17.

We conclude that it is the hypergeometric distribution:

a) h(x; 6, 9, 17).

b)

`P[X=2]=\frac{(^(g)C_(2))^(17-9)C_(6-2)}{^(17)C_(6)\textrm{}}`

P[X=2] = 0.2036

P[X ≤ 2] = P(x=0)+ P(x=1) + P(x=2)

P[X ≤ 2] = 0.2466

P[X ≥ 2] = 1-[P(x=0)+P(x=1)]

P[X ≥ 2] = 0.9570.

c)

Mean=
`n(K)/(N)`

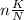
= 3.176.

Variance =
`n(K)/(N)( (N-K)/(N))((N-n)/(n-1) )`

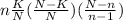
= 2.824 x 0.6471 x 0.5625

= 1.028.

Standard deviation =
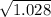`√(1.028)` = 1.014.