Answer:
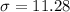 --- Standard deviation
--- Standard deviation
Explanation:
Given
See attachment for graph
Solving (a): Explain how the standard deviation is calculated.
Start by calculating the mean
To do this, we divide the sum of the products of grade and number of students by the total number of students;
i.e.
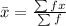
So, we have:
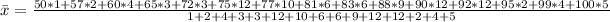
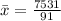
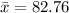
Next, calculate the variance using the following formula:
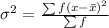
i.e subtract the mean from each dataset; take the squares; add up the squares; then divide the sum by the number of dataset
So, we have:

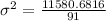
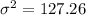
Lastly, take the square root of the variance to get the standard deviation
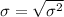
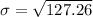
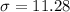 --- approximated
--- approximated
Hence, the standard deviation is approximately 11.28
Considering the calculated mean (i.e. 82.76), the standard deviation (i.e. 11.28) is small and this means that the grade of the students are close to the average grade.