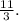Final answer:
The series
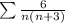 is convergent as a telescoping sum, and its sum is
is convergent as a telescoping sum, and its sum is
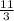 or approximately 3.67.
or approximately 3.67.
Step-by-step explanation:
The question asks to determine whether the series
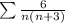 from n = 1 to infinity converges or diverges. To solve this, we will express the general term as a difference of two fractions that will telescope when we add the terms of the series.
from n = 1 to infinity converges or diverges. To solve this, we will express the general term as a difference of two fractions that will telescope when we add the terms of the series.
To start, notice that n(n + 3) can be written as (n + 3) - n. This allows us to decompose the general term an =
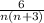 using partial fraction decomposition:
using partial fraction decomposition:
![\[(6)/(n(n + 3)) = (A)/(n) + (B)/(n + 3)\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/3fxawmb9sy8t7e4td033ulv9kl45hz3mj2.png)
By finding constants A and B (which turn out to be A = 2 and B = -2), the series becomes:
![\[(2)/(n) - (2)/(n + 3)\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/15rds66uxr2k6j498jlg5iziwy0i47qhnc.png)
As we sum an from n = 1 to infinity, the terms will cancel out in a telescoping fashion. The sum becomes:
![\[S = ((2)/(1) - (2)/(4)) + ((2)/(2) - (2)/(5)) + ((2)/(3) - (2)/(6)) + \ldots\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/xmqyx4dk80qh4jan2tqcdhk3jbanssmwom.png)
Most terms will cancel, and what we're left with are the first three terms of the numerator: 2 + 1 +
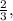 which equals
which equals
 or approximately 3.67. Thus, the series is convergent and its sum is
or approximately 3.67. Thus, the series is convergent and its sum is