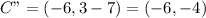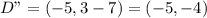Answer:
See explanation
Explanation:
The question is incomplete, as some coordinates to transform are not given.
I will, however, give a general explanation.
Rotate circle 270 degrees counterclockwise
This implies that, we rotate the center of the circle and the rule of this rotation is:
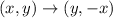
Assume the center is: (5,3), the new center will be: (3,-5)
Reflect square across y-axis
The rule is:
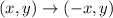
If the square has (3,5) as one of its vertices before rotation, the new point will be (-3,5).
Reflect triangle across y-axis, then 3 units up and 2 units left
The rule of reflection is:
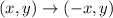
If the triangle has (3,5) as one of its vertices before rotation, the new point will be (-3,5).
The rule of translating a point up is:
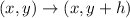 where h is the unit of translation
where h is the unit of translation
In this case, h = 3; So, we have:
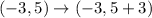
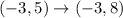
The rule of translating a point left is:
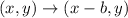 where b is the unit of translation
where b is the unit of translation
In this case, b = 2; So, we have:
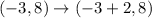
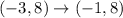
The L shape
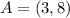
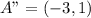
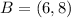
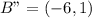
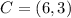
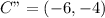
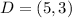
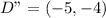
Required
The transformation from ABCD to A"B"C"D"
First, ABCD is reflected across the y-axis.
The rule is:
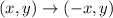
So, we have:
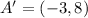
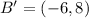
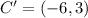
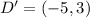
Next A'B'C'D' is translated 7 units down
The rule is:
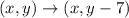
So, we have: