Question

Write an equation for a parabola that has a vertex (1, 2) and passes through the point (3, -6).

Answer 1

y= -2x²+4x.

Explanation:

the common equation of the parabola is y=ax²+bx+c, where a, b, c - numbers.

1) the coordinates of the vertex are:

`x_0=-(b)/(2a) \ and \ y_0=(4ac-b^2)/(4a).`

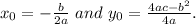
2) if according to the condition x₀=1, then b= -2a.

If according to the condition y₀=2, then
`2=(4ac-b^2)/(4a)=(4ac-4a^2)/(4a)=c-a;`

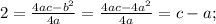
it means that c=a+2.

3) if b= -2a; c=a+2 and the point (3;-6) belongs to the given parabola, then it is possible to substitute them into the common equation of the parabola:

-6=3²*a-6a+a+2; ⇔ a= -2.

4) if a= -2, then b=-2a=4, and c=a+2=0.

5) if a=-2, b=4 and c=0, then the required equation of the parabola is:

y= -2x²+4x.