Answer:
y= -2x²+4x.
Explanation:
the common equation of the parabola is y=ax²+bx+c, where a, b, c - numbers.
1) the coordinates of the vertex are:
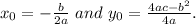
2) if according to the condition x₀=1, then b= -2a.
If according to the condition y₀=2, then
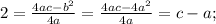
it means that c=a+2.
3) if b= -2a; c=a+2 and the point (3;-6) belongs to the given parabola, then it is possible to substitute them into the common equation of the parabola:
-6=3²*a-6a+a+2; ⇔ a= -2.
4) if a= -2, then b=-2a=4, and c=a+2=0.
5) if a=-2, b=4 and c=0, then the required equation of the parabola is:
y= -2x²+4x.