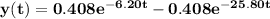Question

A hollow steel ball weighing 4 pounds is suspended from a spring. This stretches the spring 1515 feet. The ball is started in motion from the equilibrium position with a downward velocity of 88 feet per second. The air resistance (in pounds) of the moving ball numerically equals 4 times its velocity (in feet per second) . Suppose that after t seconds the ball is y feet below its rest position. Find y in terms of t. (Note that the positive direction is down.) Take as the gravitational acceleration 32 feet per second per second.

Answer 1

`\mathbf{y(t) =0.408e^(-6.20t )-0.408e^(-25.80t)}}`

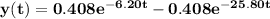
Step-by-step explanation:

Given that:

The weight of ball = 4 pounds

The spring stretch x = 1/15 feet

Using the relation of weight on an object:

W = mg

m = W/g

m = 4 / 32

m = 1/8

Now, from Hooke's law:

F = kx

4 =k(1/5)

k = 20 lb/ft

However, since the air resistance is 4 times the velocity;

Then, we can say:

C = 4

Now, for the damped vibration in the spring-mass system, we have:

`m(d^2 y)/(dx^2)+ c(dy)/(dt)+ky = 0`

`((1)/(8))(d^2 y)/(dx^2)+ 4(dy)/(dt)+20y = 0`

`(d^2 y)/(dx^2)+ 32(dy)/(dt)+160y = 0`

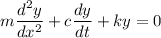
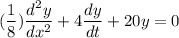
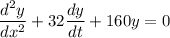
Solving the differential equation:

m² + 32m + 160 = 0

Solving the equation:

m = -25.80 or m = -6.20

So, the general solution for the equation is:

`y (t)= c_1 e^(-6.20t)+c_2e^(-25.80t)`

`y '(t)=-6.20 c_1 e^(-6.20t)-25.80c_2e^(-25.80t)`

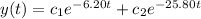
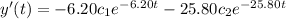
y(0) = 0 ; y'(0) = 8

`y (0)= c_1 e^(-6.20(0))+c_2e^(-25.80(0))`

`c_1 +c_2 = 0 ---(1)`

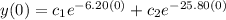
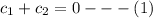
At y'(0) = 8

`y '(0)=-6.20 c_1 e^(-6.20(0))-25.80c_2e^(-25.80(0)) \\ \\ 8=-6.20 c_1 e^(0)-25.80c_2e^(0) \\ \\ 8=-6.20 c_1 -25.80c_2--- (2)`

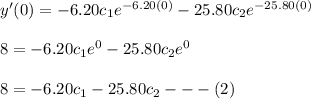
From (1), let
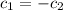`c_1 = -c_2`, then replace the value of c_1 into equation (2)

`8=-6.20 (-c_2)-25.80c_2`

`8=6.20c_2-25.80c_2`

`8=-19.60c_2`

`c_2=( 8)/(-19.60)`

`c_2 = -0.408`

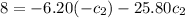
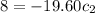
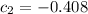
From
`c_1 = -c_2`

`c_1 = -(-0.408)`

`c_1 = 0.408`

∴

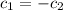
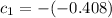
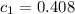
The required solution in terms of t is:

`\mathbf{y(t) =0.408e^(-6.20t )-0.408e^(-25.80t)}}`