Question

The lengths of pregnancies are normally distributed with a mean of days and a standard deviation of days. a. Find the probability of a pregnancy lasting days or longer. b. If the length of pregnancy is in the lowest ​%, then the baby is premature. Find the length that separates premature babies from those who are not premature.

Answer 1

a) The probability of a pregnancy lasting X days or longer is given by 1 subtracted by the p-value of
`Z = (X - \mu)/(\sigma)`, in which
`\mu` is the mean and
`\sigma` is the standard deviation.

b) We have to find X when Z has a p-value of
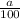`(a)/(100)`, and X is given by:
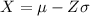`X = \mu - Z\sigma`, in which
`\mu` is the mean and
`\sigma` is the standard deviation.

Explanation:

Normal Probability Distribution

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

In this question:

Mean
`\mu`, standard deviation
`\sigma`

a. Find the probability of a pregnancy lasting X days or longer.

The probability of a pregnancy lasting X days or longer is given by 1 subtracted by the p-value of
`Z = (X - \mu)/(\sigma)`, in which
`\mu` is the mean and
`\sigma` is the standard deviation.

b. If the length of pregnancy is in the lowest a​%, then the baby is premature. Find the length that separates premature babies from those who are not premature.

We have to find X when Z has a p-value of
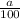`(a)/(100)`, and X is given by:
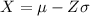`X = \mu - Z\sigma`, in which
`\mu` is the mean and
`\sigma` is the standard deviation.