Question

Classify the following polynomials. Combine any

like terms first.
x^2+3x + 2x - 2x^2
X^3+ 4x - 4x - 4x^2
X^3+2x - X^3- 2x^2+ 3

Answer 1

First simplify all polynomials and rewrite them in descending exponent order.

1.
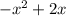
`-x^2+2x`

2.
`x^3-4x^2`

3.
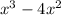
`-2x^2+2x+3`

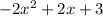
Now observe the terms with highest exponents in each expression, in particularly focus on their exponent value,

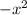`-x^2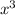` with value of 2

`x^3` with value of 3

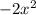`-2x^2` with value of 2

The value is also known as order of polynomial and it is a way to classify polynomials.

Every order creates a family of polynomials determined by the order (which is always greater than -1)

A polynomial such as (1) and (3) have an orders of 2, which is often called quadratic order and thus the polynomials (1), (3) are classified in the same family of quadratic polynomials, these are polynomials with order of 2.

Polynomial (2) however has an order of 3, which is called cubic order. This polynomial (2) is classified in the family of cubic polynomials.

There are of course many other families, in fact, infinitely many of them because you have order 0, 1, 2, 3, and so on there are precisely
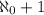`\aleph_0+1` read as "aleph 0 + 1" (the number of natural numbers + 1 (because 0 is not a natural number)) of polynomial families.

The first few have these fancy names, for example:

order 0 => constant polynomial

order 1 => linear polynomial

order 2 => quadratic polynomial

order 3 => cubic polynomial

order 4 => quartic polynomial

and so on.

Hope this helps!