Answer:
Step-by-step explanation:
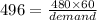
demand per day = 58 pans
Due to availability of two workers we can have parallel we can have deep drawing and trimming operations simultaneously.
Hence the cycle time would be the greater time of the two operations.
cycle time = 450 seconds
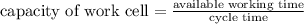
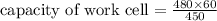
 (which is greater than the demand of 58 pans)
(which is greater than the demand of 58 pans)
Therefore the work cell has sufficient capacity and time (496 sec.>cycle time 450 sec) to meet the demand.
b)
Required daily production is 58 pans