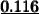Answer:
0. 116
Explanation:
The function is given as :-
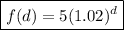
and we have to find the rate of change from d = 4 to d = 11
![\boxed{\blue{\mathfrak{Rate\: of\: change = (final\:output-intital\:output)/(final\:input-initial\:input) } }}]()
The final input value is 11 whereas the initial input value is 4.
The final and initial outputs can be calculated by placing the respective values of initial and final inputs (that are 4 and 11).
f(4) =

f(4) = 5 × 1. 08
f(4) = 5. 41
f(11) =
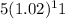
f(11) = 5 × 1. 24
f(11) = 6. 22
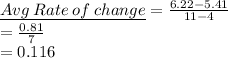
 Hence, the average rate of change is
Hence, the average rate of change is