Given:
The x- intercepts of a parabola are (0,-6) and (0,4).
The parabola crosses the y- axis at -120.
Lucas said that an equation for the parabola is
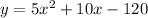 and that the coordinates of the vertex are (-1, -125).
and that the coordinates of the vertex are (-1, -125).
To find:
Whether Lucas is correct or not.
Solution:
The x- intercepts of a parabola are (0,-6) and (0,4). It means (x+6) and (x-4) are the factors of the equation of the parabola.
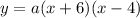 ...(i)
...(i)
The parabola crosses the y- axis at -120. It means the equation of the parabola must be true for (0,-120).
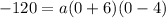
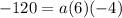
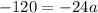
Divide both sides by -24.

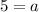
Substituting
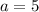 in (i), we get
in (i), we get
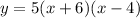
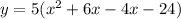

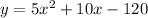
So, the equation of the parabola is
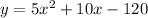 .
.
The vertex of a parabola
 is:
is:
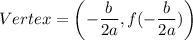
In the equation of the parabola,
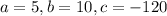 .
.
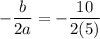
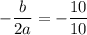

Putting
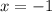 in the equation of the parabola, we get
in the equation of the parabola, we get
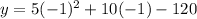
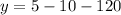

So, the vertex of the parabola is at point (-1,-125).
Therefore, Lucas is correct.