Question

Find the perimeter of WXYZ. Round to the nearest tenth if necessary.

Answer 1

Answer:CCCCCCCCCCCCCCCCC

Explanation:

Answer 2

C. 15.6

Explanation:

Perimeter of WXYZ = WX + XY + YZ + ZW

Use the distance formula,
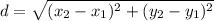`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)` to calculate the length of each segment.

✔️Distance between W(-1, 1) and X(1, 2):

Let,

`W(-1, 1) = (x_1, y_1)`

`X(1, 2) = (x_2, y_2)`

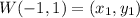
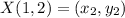
Plug in the values

`WX = √((1 - (-1))^2 + (2 - 1)^2)`

`WX = √((2)^2 + (1)^2)`

`WX = √(4 + 1)`

`WX = √(5)`

`WX = 2.24`

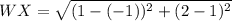
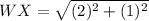
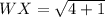
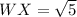
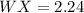
✔️Distance between X(1, 2) and Y(2, -4)

Let,

`X(1, 2) = (x_1, y_1)`

`Y(2, -4) = (x_2, y_2)`

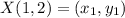
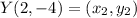
Plug in the values

`XY = √((2 - 1)^2 + (-4 - 2)^2)`

`XY = √((1)^2 + (-6)^2)`

`XY = √(1 + 36)`

`XY = √(37)`

`XY = 6.08`

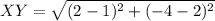
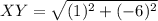
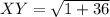
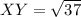
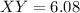
✔️Distance between Y(2, -4) and Z(-2, -1)

Let,

`Y(2, -4) = (x_1, y_1)`

`Z(-2, -1) = (x_2, y_2)`

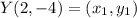
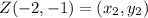
Plug in the values

`YZ = √((-2 - 2)^2 + (-1 -(-4))^2)`

`YZ = √((-4)^2 + (3)^2)`

`YZ = √(16 + 9)`

`YZ = √(25)`

`YZ = 5`

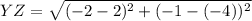
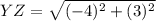
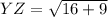
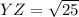
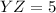
✔️Distance between Z(-2, -1) and W(-1, 1)

Let,

`Z(-2, -1) = (x_1, y_1)`

`W(-1, 1) = (x_2, y_2)`

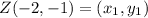
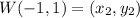
Plug in the values

`ZW = √((-1 -(-2))^2 + (1 - (-1))^2)`

`ZW = √((1)^2 + (2)^2)`

`ZW = √(1 + 4)`

`ZW = √(5)`

`ZW = 2.24`

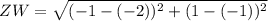
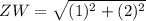
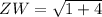
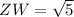
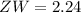
✅Perimeter = 2.24 + 6.08 + 5 + 2.24 = 15.56

≈ 15.6