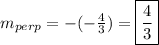Answer:
4/3
Explanation:
In slope-intercept form
 ,
,
 represents the slope of the line.
represents the slope of the line.
Let's write
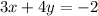 in slope-intercept form by isolating
in slope-intercept form by isolating
 :
:
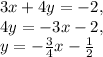
Therefore, the slope of this line is
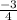 . To find the slope of a line perpendicular to it, multiply the reciprocal of the slope by -1 (take the negative reciprocal).
. To find the slope of a line perpendicular to it, multiply the reciprocal of the slope by -1 (take the negative reciprocal).
Therefore, the slope of a line perpendicular to
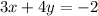 is:
is: