Answer:

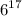
Explanation:
Question-1:
we want to rewrite the following expression as an exponent

remember that 25 is the square of 5 therefore
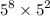
recall that,
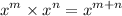
with that law we obtain:

simplify addition:

Question-2:
likewise Question-1 36 is the square of 6 Thus,
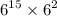
similarly apply law of exponent:
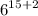
simplify addition:
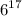
hence,
we have written the expression as an exponent