Answer:
f(x) is shrinked
Explanation:
Given
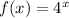
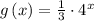
Required
The effect of dilation on f(x)
From the given parameters, we have:
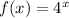
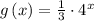
On a general term;
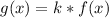
So by comparison:
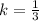
When scale of dilation is less than 1, it means the function is reduced. Hence, the specific effect on f(x) is shrink