Question

If your weight is 588N on the earth, how far should you go from the centre of the earth so that your weight will be 300N? The radius of the earth is 6400km and the value of g on the earth surface is 9.8m/s2. please explain....​

Answer 1

Step-by-step explanation:

You need something that relates distance to what the gravitational pull is. You can set up a complex sort of proportion. What you need is a number that is comparable to 9.81 or you can just use the Gravitational Force formula with a 4 tier fraction.

Givens

x = the additional distance toward outer space above the radius of the earth.

G is the gravitational constant.

m1 = the person's mass (which does not change no matter where you are).

m2 = the earth's mass

F1 = 588 N

F2 = 300 N

Formula

`(F1)/(F2) = (588 N)/(300N)=((Gm1*m2/)/(6400^2) )/((G*m1*m2)/((6400 + x)^2) )`

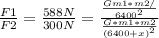
Solution

G*m1*m2 all cancel. So what you get looks like this.

`(588)/(300) = ((6400 + x)^2)/(6400^2)`

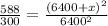
Cross Multiply

588 * 6400^2 = 300*(6400+x)^2 Now all you need do is solve for x.

x will be in km.

588*40960000 = 300 * (40960000 + 12800x + x^2)

1.2288*10^10 + 3840000x + 300x^2 = 2.408448*10^10

300x^2 + 3840000x + 1.2288*10^10 = 2.408448 * 10^10

Subtract 2.409448 * 10^10 from both sides.

300x^2 + 3840000x - 1,179648 * 10^10

Now use the quadratic formula

I'm guessing I should have converted this to meters because I'm getting ridiculous numbers. They are already large enough as you can see. The method is correct, even if the numbers are not.