Question

Suppose the mean income of firms in the industry for a year is 95 million dollars with a standard deviation of 11 million dollars. If incomes for the industry are distributed normally, what is the probability that a randomly selected firm will earn less than 114 million dollars

Answer 1

95.73%

Explanation:

Given data:

mean μ= 95

standard deviation, σ = 11

to calculate, the probability that a randomly selected firm will earn less than 114 million dollars;

Use normal distribution formula

`P(X<114)=P(Z<(X-\mu)/(\sigma) )`

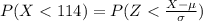
Substitute the required values in the above equation;

`P(X<114)=P(Z<(114-95)/(11) )\\P(X<114)=P(Z<1.7272)\\P(X<114)=0.9573`

Therefore, the probability that a randomly selected firm will earn less than 114 million dollars = 95.73%