Answer:
B
Explanation:
Given that y varies inversely with x then the equation relating them is
y =
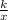 ← k is the constant of variation
← k is the constant of variation
To find k use the condition y = 18 when x = 12 , then
18 =
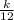 ( multiply both sides by 12 )
( multiply both sides by 12 )
216 = k
y =
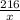 ← equation of variation
← equation of variation
When y = 24 , then
24 =
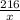 ( multiply both sides by x )
( multiply both sides by x )
24x = 216 ( divide both sides by 24 )
x = 9