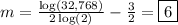Question

8^5 = 2^2m+3


Solve m

Answer 1

`m=6`

Explanation:

Exponent properties:

We can use exponent property
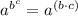`a^(b^c)=a^((b\cdot c))` to solve this problem.

Rewrite
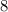`8` as
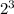`2^3`, then apply exponent property
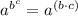`a^(b^c)=a^((b\cdot c))` to simplify:

`2^(3^5)=2^(2m+3),\\2^(15)=2^(2m+3)`

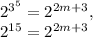
If
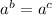`a^b=a^c`, then
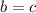`b=c`, because of log property
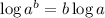`\log a^b=b\log a`. Using this log property, you can take the log of both sides and divide by
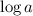`\log a` to get
`b=c`

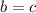
Therefore, we have:

`15=2m+3`

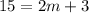
Subtract 3 from both sides:

`12=2m`

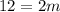
Divide both sides by 6:

`m=(12)/(2)=\boxed{6}`

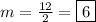
Alternative:

Given
`8^5=2^(2m+3)`, to move the exponent down, we'll use log properties.

Start by simplifying:

`\log 32,768=2^(2m+3)`

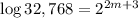
Take the log of both sides, then use log property
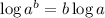`\log a^b=b\log a` to move the exponent down:

`\log(32,768)=\log 2^(2m+3),\\\log (32,768)=(2m+3)\log 2`

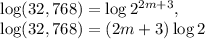
Divide both sides by
`\log2`:

`2m+3=(\log (32,768))/(\log(2))`

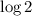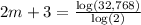
Subtract 3 from both sides:

`2m=(\log (32,768))/(\log(2))-3`

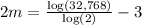
Divide both sides by 2:

`m=(\log (32,768))/(2\log(2))-(3)/(2)=\boxed{6}`