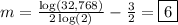Answer:
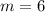
Explanation:
Exponent properties:
We can use exponent property
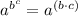 to solve this problem.
to solve this problem.
Rewrite
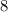 as
as
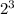 , then apply exponent property
, then apply exponent property
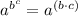 to simplify:
to simplify:
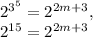
If
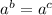 , then
, then
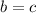 , because of log property
, because of log property
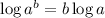 . Using this log property, you can take the log of both sides and divide by
. Using this log property, you can take the log of both sides and divide by
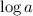 to get
to get
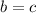
Therefore, we have:
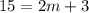
Subtract 3 from both sides:
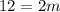
Divide both sides by 6:
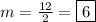
Alternative:
Given
 , to move the exponent down, we'll use log properties.
, to move the exponent down, we'll use log properties.
Start by simplifying:
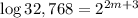
Take the log of both sides, then use log property
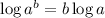 to move the exponent down:
to move the exponent down:

Divide both sides by
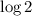 :
:
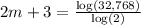
Subtract 3 from both sides:
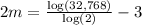
Divide both sides by 2: