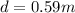Question

A 67.3-kg climber is scaling the vertical wall of a mountain. His safety rope is made of a material that, when stretched, behaves like a spring with a spring constant of 1.23 x 103 N/m. He accidentally slips and falls freely for 0.921 m before the rope runs out of slack. How much is the rope stretched when it breaks his fall and momentarily brings him to rest

Answer 1

`d=0.59m`

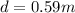
Step-by-step explanation:

From the question we are told that:

Mass
`m=67.3 kg`

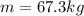
Spring constant
`\mu=1.23 * 10^3 N/m`

Fall Height
`h=0.921m`

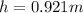
Generally the Energy theorem equation for momentum is mathematically given by

Change in KE=Work done by gravity + work done by spring

`0=mg*(h + d) - (\mu d^2)/(2)`

`0=(67.3 * 9.81 (0.921 + d)) -((1.23 * 10^3 * d^2)/( 2)`

`0=608.1-660.213d-615d^2`

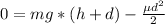
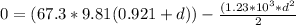
Solving Quadratic equation

`d=0.59m`