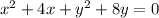Answer:
Explanation:
Given

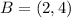
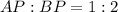
Required
The locus of P
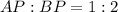
Express as fraction
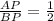
Cross multiply

Calculate AP and BP using the following distance formula:

So, we have:

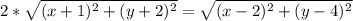
Take square of both sides
![4 * [(x +1)^2 + (y +2)^2] = (x - 2)^2 + (y - 4)^2](https://img.qammunity.org/2022/formulas/mathematics/college/sz8fonbzkb6xa66ajekkaugrg8k6buz8uu.png)
Evaluate all squares
![4 * [x^2 + 2x + 1 + y^2 +4y + 4] = x^2 - 4x + 4 + y^2 - 8y + 16](https://img.qammunity.org/2022/formulas/mathematics/college/sm3i0l84fuwo5jz1doir0n22obnpnbl9p2.png)
Collect and evaluate like terms
![4 * [x^2 + 2x + y^2 +4y + 5] = x^2 - 4x + y^2 - 8y + 20](https://img.qammunity.org/2022/formulas/mathematics/college/wp9wsxq0ooo3zn9svpzn9gim45gkqdankj.png)
Open brackets
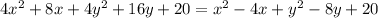
Collect like terms
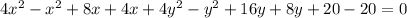
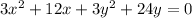
Divide through by 3