Answer:
Explanation:
We'll start with going form exponential to radical, since it may be easier to follow. For example,
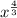 can be written, in radical form, as
can be written, in radical form, as
![\sqrt[3]{x^4}](https://img.qammunity.org/2022/formulas/mathematics/high-school/4jhfvhreu70y94fhgmrghxgyvgzx580htf.png) . What happens is that the denominator of the fraction serves as the index (the number that sits in the bend of the radical) and the numerator serves as the power on the variable (or number, if that's the case). Let's look at another one:
. What happens is that the denominator of the fraction serves as the index (the number that sits in the bend of the radical) and the numerator serves as the power on the variable (or number, if that's the case). Let's look at another one:
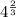 becomes
becomes
![\sqrt[3]{4^2}=\sqrt[3]{16}=\sqrt[3]{8*2}=2\sqrt[3]2}](https://img.qammunity.org/2022/formulas/mathematics/high-school/undppqsejlkwpgpw2nm19shbp366jg2hxm.png)
And you can go the other way with it. For example,
![\sqrt[5]{x^4}](https://img.qammunity.org/2022/formulas/mathematics/college/hbihunugd0srbxtr3g766qjmnjtc4whgs6.png) becomes
becomes
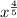 , etc. Get it?
, etc. Get it?