Question

What is the coefficient of x3 in the expansion of (2x−3)5?

Group of answer choices

a) -360

b) 720

c) 10

d) -5

e) -120

Answer 1

B 720

Explanation:

same process as the previous image I sent ya

Answer 2

B) 720.

Explanation:

We can use the Binomial Expansion Theorem:

`\displaystyle (a+b)^n=\sum_(k=0)^(n)\binom{n}{k}a^kb^(n-k)`

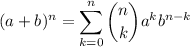
We have the expression:

`\displaystyle (2x-3)^5`

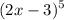
Therefore, a = 2x, b = -3, and n = 5.

We want to find the coefficient of x³. To get x³, we can cube a. Therefore, we can find our coefficient by letting k = 3. Hence:

`\displaystyle \binom{5}{3}(2x)^3(-3)^(5-3)`

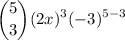
Evaluate:

`\displaystyle =10(8x^3)(9)=720x^3`

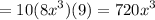
Our answer is B.