Answer:
B) 720.
Explanation:
We can use the Binomial Expansion Theorem:

We have the expression:
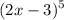
Therefore, a = 2x, b = -3, and n = 5.
We want to find the coefficient of x³. To get x³, we can cube a. Therefore, we can find our coefficient by letting k = 3. Hence:
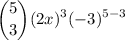
Evaluate:
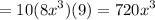
Our answer is B.