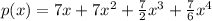Question

Use the definition of a Taylor series to find the first four nonzero terms of the series for f(x) centered at the given value of a.

f(x)= 7x e^x, a= 0

Answer 1

Hi there!

`\large\boxed{p(x) = 7x + 7x^2 + (7)/(2)x^3 + (7)/(6)x^4}`

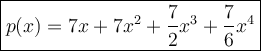
Recall a Taylor series centered at x = 0:

`p(x) = f(0) + f'(0)(x) + (f''(0))/(2)x^(2) + (f'''(0))/(3!)x^(3) + ...+ (f^n)/(n!)x^n`

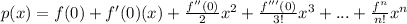
Begin by finding the derivatives and evaluate at x = 0:

f(0) = 7(0)e⁰ = 0

f'(x) = 7eˣ + 7xeˣ f'(0) = 7e⁰ + 7(0)e⁰ = 7

f''(x) = 7eˣ + 7eˣ + 7xeˣ f''(0) = 7(1) + 7(1) + 0 = 14

f'''(x) = 7eˣ + 7eˣ + 7eˣ + 7xeˣ f'''(0) = 21

f⁴(x) = 7eˣ + 7eˣ + 7eˣ + 7eˣ + 7xeˣ f⁴(0) = 28

Now that we calculated 4 non-zero terms, we can write the Taylor series:

`p(x) = 0 + 7x + (14)/(2)x^2 + (21)/(3!)x^3 + (28)/(4!)x^4`

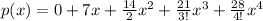
Simplify:

`p(x) = 7x + 7x^2 + (7)/(2)x^3 + (7)/(6)x^4`