Answer:
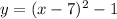
Explanation:
We want to convert the equation:
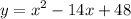
Into vertex form, given by:
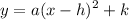
Where a is the leading coefficient and (h, k) is the vertex.
There are two methods of doing this. We can either: (1) use the vertex formulas or (2) complete the square.
Method 1) Vertex Formulas
Let's use the vertex formulas. First, note that the leading coefficient a of our equation is 1.
Recall that the vertex is given by:
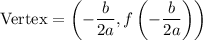
In this case, a = 1, b = -14, and c = 48. Find the x-coordinate of the vertex:
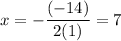
To find the y-coordinate, substitute this value back into the equation. Hence:
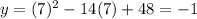
Therefore, our vertex (h, k) is (7, -1), where h = 7 and k = -1.
And since we already determined a = 1, our equation in vertex form is:
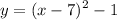
Method 2) Completing the Square
We can also complete the square to acquire the vertex form. We have:
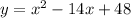
Factor out the leading coefficient from the first two terms. Since the leading coefficient is one in this case, we do not need to do anything significant:
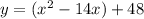
Now, we half b and square it. The value of b in this case is -14. Half of -14 is -7 and its square is 49.
We will add this value inside the parentheses. Since we added 49 inside the parentheses, we will also subtract 49 outside to retain the equality of the equation. Hence:
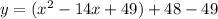
Factor using the perfect square trinomial and simplify:
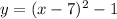
We acquire the same solution as before, with the vertex being (7, -1).