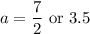Answer:
Explanation:
We have the two points (3a, 4) and (a, -3).
And we want to find the value of a such that the gradient of the line joining the two points is 1.
Recall that the gradient or slope of a line is given by the formula:

Where (x₁, y₁) is one point and (x₂, y₂) is the other.
Let (3a, 4) be (x₁, y₁) and (a, -3) be (x₂, y₂). Substitute:
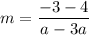
Simplify:
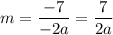
We want to gradient to be one. Therefore, m = 1:
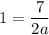
Solve for a. Rewrite:
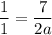
Cross-multiply:
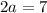
Therefore: