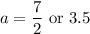Question

Find the value of a if the line joining the points (3a,4) and (a, -3) has a gradient of 1 ?

Answer 1

`(7)/(2)`

Explanation:

Objective: Linear Equations and Advanced Thinking.

If a line connects two points (3a,4) and (a,-3) has a gradient of 1. This means that the slope formula has to be equal to 1

If we use the points to find the slope: we get

`(4 + 3)/(3a - a)`

Notice how the numerator is 7, this means the denominator has to be 7. This means the denomiator must be 7.

`3a - a = 7`

`2a = 7`

`a = (7)/(2)`

Answer 2

`\displaystyle a=(7)/(2)\text{ or } 3.5`

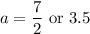
Explanation:

We have the two points (3a, 4) and (a, -3).

And we want to find the value of a such that the gradient of the line joining the two points is 1.

Recall that the gradient or slope of a line is given by the formula:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

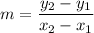
Where (x₁, y₁) is one point and (x₂, y₂) is the other.

Let (3a, 4) be (x₁, y₁) and (a, -3) be (x₂, y₂). Substitute:

`\displaystyle m=(-3-4)/(a-3a)`

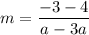
Simplify:

`\displaystyle m=(-7)/(-2a)=(7)/(2a)`

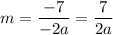
We want to gradient to be one. Therefore, m = 1:

`\displaystyle 1=(7)/(2a)`

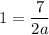
Solve for a. Rewrite:

`\displaystyle (1)/(1)=(7)/(2a)`

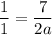
Cross-multiply:

`2a=7`

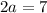
Therefore:

`\displaystyle a=(7)/(2)\text{ or } 3.5`