Answer:
Expected value =0.9
Standard deviation = 0.4359
Explanation:
Let's use the formula to find expected value or mean.
Expected value =Σ x *P(x)
x 0 1 2
P(x) ) .15 .8 .05
So, expected value = (0)(0.15) +1(0.8)+2(0.05)
= 0 +0.8 +0.1
=0.9
Expected value =0.9
Now, let's find standard deviation
x
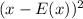
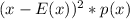
0
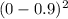
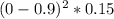 =0.1215
=0.1215
1
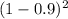
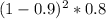 =0.008
=0.008
2
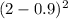
 =0.0605
=0.0605
Now, add the last column together and then take square root to find standard deviation.
Standard deviation of the distribution =
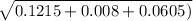
Simplify it, so standard deviation =0.4358898...
Round the answer to nearest four decimal places
Standard deviation = 0.4359