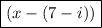Question

If a polynomial function f(x) has roots -9 and 7-i, what must be a factor of f(x)

(x-(7+i))
(x-(-7-i))
(x+(7+i))
(x+(7-i))

Answer 1

f(x) = [x-(7-2i)][x-(7+2i)]

= [(x-7)+2i][(x-7)-2i]

= (x-7)2 - (2i)2

= x2 - 14x + 49 - 4i2 = x2 - 14x + 49 +4

= x2 - 14x + 53

Answer 2

`(x-(7-i))`

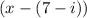
Explanation:

For a polynomial with roots
`a` and
`b`, the polynomial
`f(x)` can be written in factored form
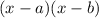`(x-a)(x-b)`. That way, when you plug in any of the roots,
`f(x)` returns zero.

Since the polynomial has at least two roots-9 and 7-i, two of its factors must then be:

`(x-(-9)\implies (x+9)\\(x-(7-i))\impli`

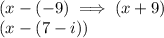
Therefore, the desired answer is
`\boxed{(x-(7-i))}`