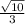Answer:
Explanation:
Point 1 (
 ,
,
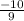 ) in the form (x1,y1)
) in the form (x1,y1)
Point 2 (
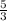 ,
,
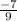 ) in the form (x2,y2)
) in the form (x2,y2)
use the distance formula
dist = sqrt[ (x2-x1)^2 + (y2-y1)^2 ]
dist = sqrt [
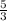 -
-
 )^2 + (
)^2 + (
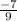 - (
- (
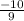 ) )^2 ]
) )^2 ]
dist = sqrt [ (
 )^2 + (
)^2 + (
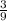 )^2 ]
)^2 ]
dist = sqrt [ 1 + (
 )^2 ]
)^2 ]
dist = sqrt [
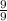 +
+
 ]
]
dist =
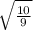
dist =
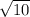 *
*
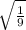
dist =
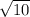 *
*

dist =