Question

g Steel plates (AISI 1010) of 4 cm thickness initially at a uniform temperature of 500 deg C are cooled by air at 50 deg C with a convection coefficient of 30 W-m2-K-1. Estimate the time it will take for their midplane temperature to reach 100 deg C.

Answer 1

Characteristic length = thickness / 2

`$=(0.04)/(2)$`

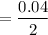
= 0.02 m

Thermal conductivity for steel is 42.5 W/m.K

`$\text{Biot number} = \frac{\text{convective heat transfer coefficient} * \text{characteristic length}}{\text{thermal conductivity}}$`

`$=(30 * 0.02)/(42.5)$`

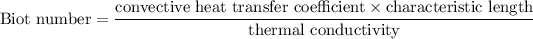
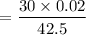
= 0.014

Since the Biot number is less than 0.01, the lumped system analysis is applicable.

`$(T-T_(\infty))/(T_0-T_(\infty)) = e^(-b* t)$`

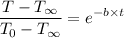
Where,

T = temperature after t time

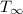`$T_(\infty)$` = surrounding temperature

`$T_0$` = initial temperature

`$b=\frac{\text{heat transfer coefficient}}{\text{density} * {\text{specific heat } * \text{characteristic length }}}$`

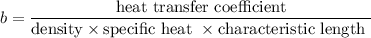
t = time

We calculate B:

`$b=(30)/(7833 * 460 * 0.02)$`

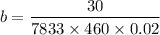
= 0.000416

Thus,
`$(100-50)/(500-50)=e^(-0.00416 * t)$`

t = 5281.78 second

= 88.02 minutes

Thus the time taken for reaching 100 degree Celsius is 88.02 minutes.