Solution :
Characteristic length = thickness / 2
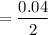
= 0.02 m
Thermal conductivity for steel is 42.5 W/m.K
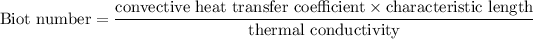
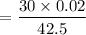
= 0.014
Since the Biot number is less than 0.01, the lumped system analysis is applicable.
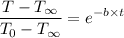
Where,
T = temperature after t time
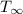 = surrounding temperature
= surrounding temperature
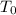 = initial temperature
= initial temperature
t = time
We calculate B:
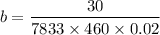
= 0.000416
Thus,
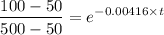
t = 5281.78 second
= 88.02 minutes
Thus the time taken for reaching 100 degree Celsius is 88.02 minutes.