Given:
The table of values for the function f(x).
To find:
The values
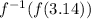 and
and
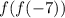 .
.
Solution:
From the given table, it is clear that the function f(x) is defined as:
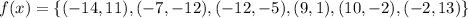
We know that if (a,b) is in the function f(x), then (b,a) must be in the function
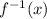 . So, the inverse function is defined as:
. So, the inverse function is defined as:
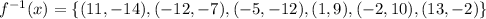
And,
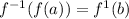
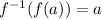 ...(i)
...(i)
Using (i), we get
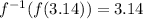
Now,
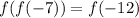
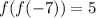
Therefore, the required values are
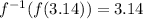 and
and
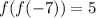 .
.