Answer:
R = (-3, 8).
Explanation:
Recall the midpoint formula:
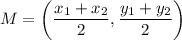
Where M is the midpoint, (x₁, y₁) is one point and (x₂, y₂) is another.
We are given that Q is the midpoint of PR, where P = (11, -2) and Q = (4, 3) and we want to find the coordinates of R.
Substitute Q for M and let P(11, -2) be (x₁, y₁). Hence:
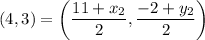
Split into two separate equations:
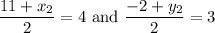
Solve for each case:
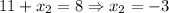
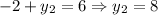
Therefore, our second point (x₂, y₂) is (-3, 8).
Hence, R = (-3, 8).