Answer:
504 arrangements are possible
Explanation:
Arrangements of n elements:
The number of arrangements of n elements is given by:
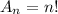
Arrangements of n elements, divided into groups:
The number of arrangements of n elements, divided into groups of
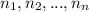 elements is given by:
elements is given by:
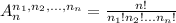
In this case:
9 pens, into groups of 5, 3 and 1. So
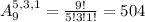
504 arrangements are possible