Question

For a project in his Geometry class, Tyler uses a mirror on the ground to measure the height of his school building. He walks a distance of 14.65 meters from his school, then places a mirror on flat on the ground, marked with an X at the center. He then steps 0.8 meters to the other side of the mirror, until he can see the top of the school clearly marked in the X. His partner measures the distance from his eyes to the ground to be 1.15 meters. How tall is the school? Round your answer to the nearest hundredth of a meter.

Answer 1

The height of the school building is approximately 21.06 meters

Explanation:

The method of Geometry Tyler is using to determine the height of his school building is through the property that similar triangles have a common ratio of corresponding their sides

The given parameters for the triangle formed by Tyler and the mirror are;

The distance from Tyler's eyes to the ground = 1.15 meters

The horizontal distance between Tyler and the mirror at X = 0.8 m

The parameters of the triangle formed by the height, h, of the school building and the mirror at X are;

The horizontal distance between the school building and the mirror = 14.65 m

The height of the school building = h

Therefore, we have;

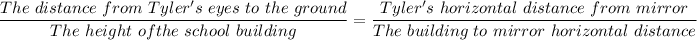`(The \ distance \ from \ Tyler's \ eyes \ to \ the \ ground)/(The \ height \ of the \ school \ building) =(Tyler's \ horizontal \ distance \ from \ mirror )/(The \ building \ to \ mirror \ horizontal \ distance )`Therefore;

`(1.15 \, m)/(h) = (0.8 \ m)/(14.65 \ m)`

`h = (1.15 \, m * 14.65 \, m )/(0.8 \, m) = 21.059375 \ m`

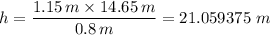
The height of the school building h to the nearest hundredth meter ≈ 21.06 m.